从双原子分子势能曲线获得光谱参数 （2.0版）

某些量化程序不能进行分子结构的几何优化，特别是激发态的几何优化。但是对于双原子分子来说，电子态的势能曲线形式简单，其中的大多数束缚态可以用Morse势函数表示，势函数中包含了光谱参数（Re, ωe, Te）的全部信息。因此，使用三次样条插值方法，处理用量化程序得到的双原子势能曲线，可以得到光谱参数。

计算方法

双原子分子电子态的势能曲线可以写成Morse势函数的形式：

                      (1)

对于基态Te是0。式中

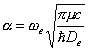                                 (2)

平衡位置Re可以通过求解下面方程获得：

                                     (3)

E(r)'是(1)式对r的一阶微分，Re点能量与基态平衡位置能量之差就是Te。

(1)式对r求二阶微分，其在r=Re处的值为

                          (4)

(2)式代入(4)式，得到力常数

                                (5)

(5)式经过变换，并经过单位换算，最后得到求ωe的公式：

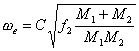                           (6)

其中，C = 5.80644 (能量和键长单位分别是cm-1-Å), 521.467 (eV-Å), 985.429 (eV-Bohr), 10.9726 (cm-1-Bohr)。在实验上，力常数f2的单位习惯取mDyne/Å，此时C = 1302.8（cm-1-Å）。
[注：计算公式为sqrt(NA*105)/2πc，其中，NA=6.022142*1023，c=2.99792458*1010 cm/s。一些文献给出的C值为1307，不准确。]

最后得到的频率ωe单位都是cm-1，M1和M2是各个原子的原子量。

因此，只要有了某个电子态的势能曲线，就可以通过以上的公式计算出光谱参数Re, ωe, Te。

应用一例

用B3LYP混合密度泛函和CEP-4G基组，计算InCl分子的基态势能曲线，并把插值拟合的结果与几何优化&频率的结果比较。密度泛函计算用Gaussian程序完成，采用默认设置。光谱常数的计算可以用商业软件Matlab或自由软件Octave完成。

　

第一步：获得InCl分子基态势能曲线。取一组等间隔键长r，间隔为Δr，计算各点相应的能量。把计算的键长-能量数据一一复制到MS Excel中。如表1.所示，键长取值间隔0.1 Å，因为程序用的hartree单位太大，能量已经换算到cm-1单位。

表1. B3LYP/CEP-4G计算的InCl分子基态能量（部分）

R(Å)

E(cm-1)

2.0

17943.568149

2.1

9659.290704

2.2

4638.411399

2.3

1713.282007

2.4

292.456480

2.5

16.534357

2.6

436.345714

2.7

1118.609743

…

...

4.4

20359.116723

4.6

21776.635378

4.8

23043.651057

5.0

24154.275915

第二步：画图。用到的Matlab命令：

x=[];输入横轴坐标。从表1.复制第一列数据，粘贴到[]中。“;”的作用是防止回显。
y=[];输入纵轴坐标。从表1.复制第二列数据，粘贴到[]中。
plot(x,y)画图。

Octave命令：

x=[输入横轴坐标。从表1.复制第一列数据，粘贴到“[”后，然后输入“];”。“;”的作用是防止回显。
y=[输入纵轴坐标。从表1.复制第二列数据，粘贴到“[”后，然后输入“];”。“;”的作用是防止回显。
plot(x,y)画图。

现在得到的势能曲线比较粗糙，无法直接用于获得光谱参数。但可以从图中初步估计平衡键长Re的位置，在2.48 Å左右。

第三步：对平衡键长Re附近的势能数据进行三次样条插值处理。插值处理区域取2.475-2.485 Å，插值间隔0.0001 Å。用到的Matlab命令：

dr=0.0001;
xi=(2.475:dr:2.485)';

产生一组等间隔的键长。在第二行命令中，第一个数值2.475是下限，第三个数值2.485是上限，dr是三次样条插值的间隔，中间用“:”隔开。后面“’”的作用是纵向排列输出结果，便于显示和复制。

yi=spline(x,y,xi);

对于势能函数y(x)，在不同的键长xi处进行三次样条插值。

plot(xi,yi)再次画图，确认能量最低点在此区域中，否则计算的光谱常数无效。

Octave命令：

dr=0.0001;
xi=(2.475:dr:2.485)';

产生一组等间隔的键长。在第二行命令中，第一个数值2.475是下限，第三个数值2.485是上限，dr是三次样条插值的间隔，中间用“:”隔开。后面“’”的作用是纵向排列输出结果，便于显示和复制。

yi=interp1(x,y,xi,'spline');

对于势能函数y(x)，在不同的键长xi处进行三次样条插值。

plot(xi,yi)再次画图，确认能量最低点在此区域中，否则计算的光谱常数无效。

第四步：寻找势能曲线的能量最低点，求解光谱常数Re（平衡键长）和Te（基态的基准能量，或激发态的激发能）。用到的Matlab命令：

te=min(yi)

yi的最小值即为Te。

re=spline(yi,xi,te)

Te对应的键长，即为Re。

Octave命令：

te=min(yi)

yi的最小值即为Te。

re=interp1(yi,xi,te,'spline')

Te对应的键长，即为Re。

第五步：计算能量二阶导，即力常数f。用到的Matlab命令：

e1=spline(xi,yi,re+dr);
e2=spline(xi,yi,re-dr);

e1和e2是Re左右两个相邻点的能量。

f=(e1+e2-te*2)/(dr*dr);用数值差分方法计算能量二阶导。

Octave命令：

e1=interp1(xi,yi,re+dr,'spline');
e2=interp1(xi,yi,re-dr,'spline');

e1和e2是Re左右两个相邻点的能量。

f=(e1+e2-te*2)/(dr*dr);用数值差分方法计算能量二阶导。

第六步：从力常数得到振动频率ωe。用到的Matlab命令：

m=115*35/(115+35);公式(6)中的InCl分子折合质量
c=5.80644;公式(6)中的常数C。这里势能函数y(x)是cm-1-Å单位
we=c*sqrt(f/m)得到振动频率

Octave命令相同。最后得到的InCl分子基态光谱参数列于表2。

表2. B3LYP密度泛函计算InCl分子基态的光谱参数。三次样条插值间隔为0.0001Å，Δr是DFT计算中分子键长取值间隔。

三次样条插值

Gaussian结果

实验值

Δr=0.1 Å

Δr=0.01 Å

Re(Å)

2.4798

2.4793

2.4793

2.4012

ωe(cm-1)

313.74

311.70

305.80

317.4

从表1可以看到，进行DFT计算的分子键长取值间隔Δr越小，结果越接近Gaussian的理论值。但是考虑到计算量的因素以及计算结果的有效数字位数，DFT计算中Δr取0.1或0.05 Å一般已经足够了。

注意：

1.这种方法不能计算反映势能曲线非谐性的ωeχe。对于浅势阱的电子态，势能曲线形状不能用Morse势函数描述。这种处理方法会使ωe和实验值有较大偏离。

2.势阱形状对Re和Te的影响不大，因此即使是浅势阱的电子态，拟合的Re和Te也是比较好的。

3.对势能曲线更高级的处理，参见LEVEL程序。

(Zork，2018.08.19更新)